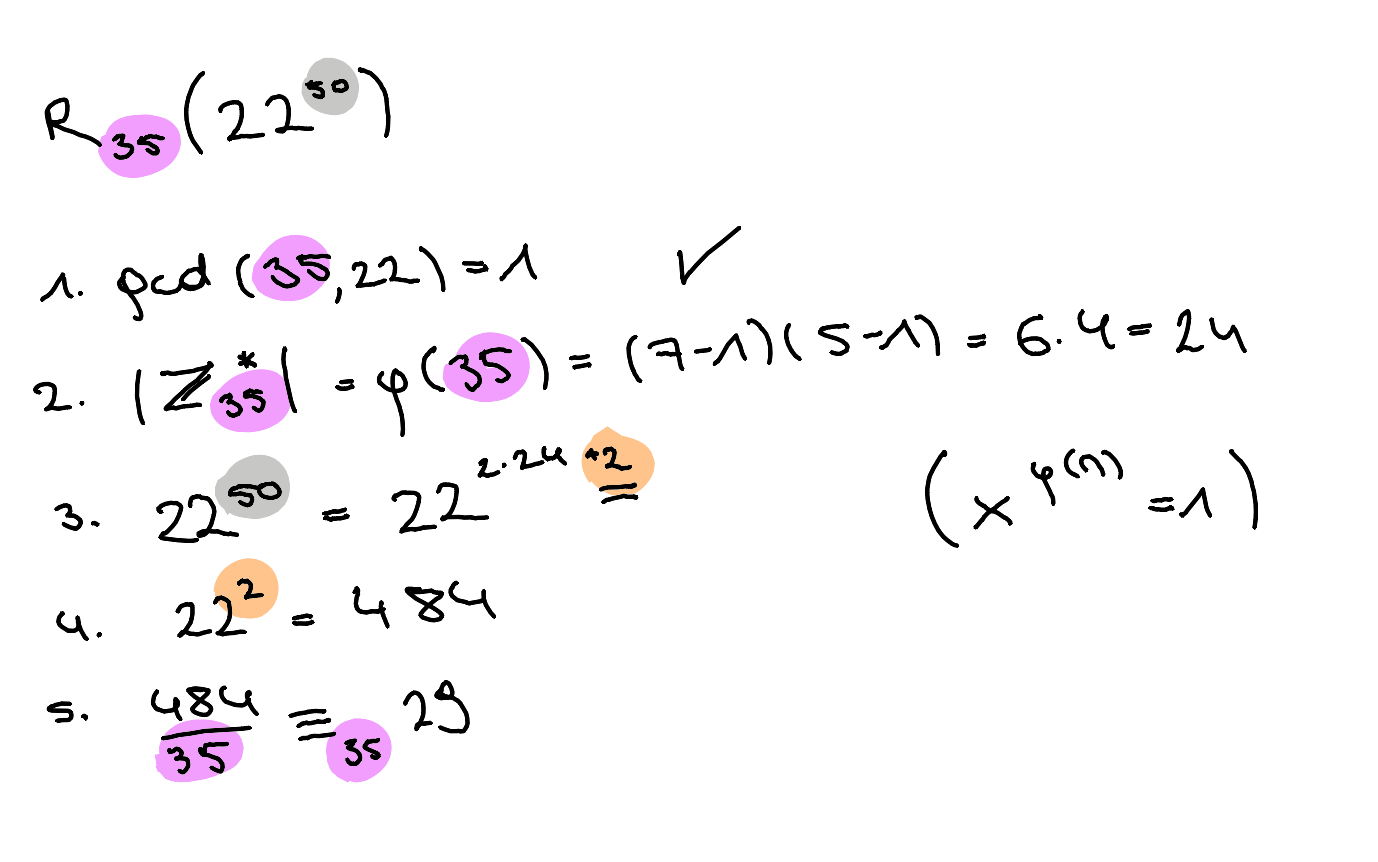$\varphi(m)=|\mathbb{Z}_{m}^*|$ (Anzahl Teilerfremd)
$\varphi(11)=10$
$\varphi(12)=4$
z.B. $\varphi(21)=(3-1)(7-1)=2\cdot 6=12$
Wenn p prim, p und q teilerfremd
- $\varphi(p)=p-1$
- $\varphi(p^i)=p^i-\frac{p^i}{p}=p^{i-1}(p-1)$ (jede p-te zahl ist nicht teilerfremd)
- $\varphi(p\cdot q)=\varphi(p)\cdot \varphi(q)$
In einer zyklischen Gruppe mit Ordnung n ist die Anzahl der Generatoren $\varphi(n)$
Satz von Euler
Rest berechnen