Hasse Diagramme
- Immer nur direkte Pfeile machen, Pfeile, die durch Transitivität erschlossen sind, wären überflüssig.
- Schlingen auslassen (da Ordnungsrelationen reflexiv)
- Transitive Kanten auslassen (da Ordnungsrelationen transitiv)
Begriffe
Kleinstes Element: Element ist related zu allen anderen. Es gibt höchstens ein minimales Element. (Beweis!)
Größtes Element: alle Elemente sind related zu diesem. Es gibt höchstens ein minimales Element. (Beweis!)
Minimales Element: es gibt kein Element, dass zu dem minimalen Element “zeigt” (mit dem related ist). Es kann mehr als ein minimales Element geben
Maximales Element: das maximale Element ist mit keinem anderen related
z.B: Teilbarkeit:
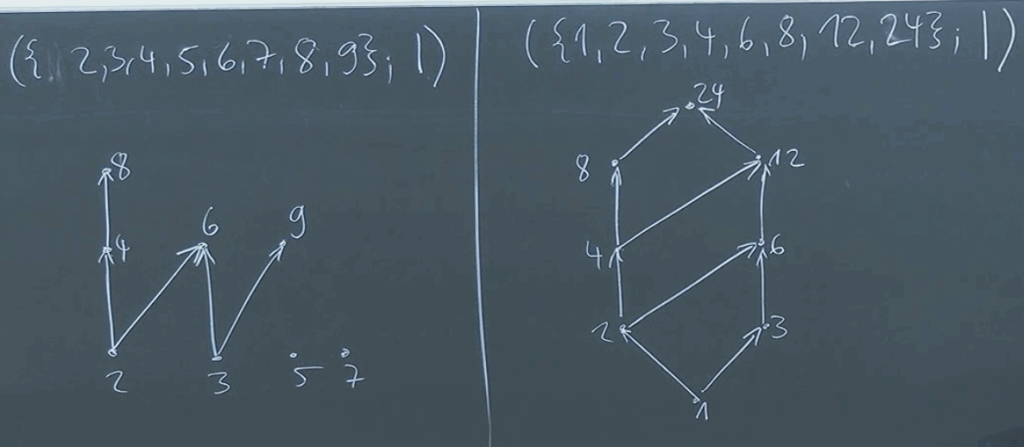

Matrix-Darstellung
(Achtung, Pfeile gehen von unten nach oben, Transitivität nutzen)
$$\begin{bmatrix}
1 & 0 & 0 & 0 \\
1 & 1 & 1 & 0 \\
0 & 0 & 1 & 0 \\
1 & 1 & 1 & 1
\end{bmatrix}$$
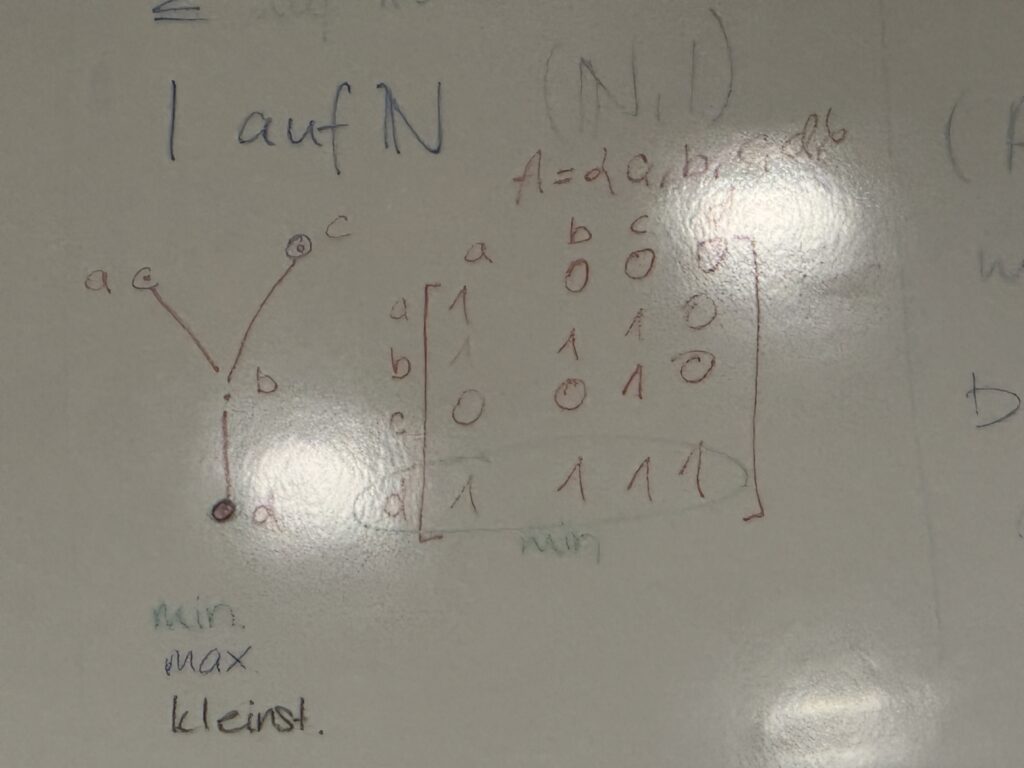
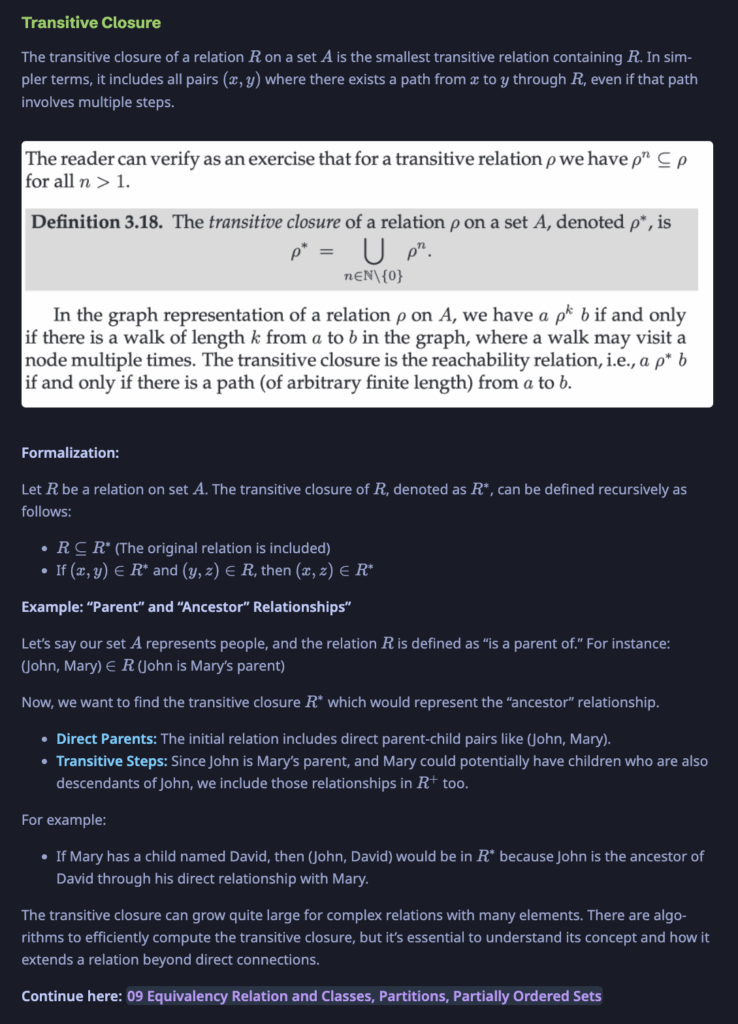
Transitive Closure
$p^1$ ist alles, was man direkt erreichen kann, $p^2$ alle Verbindungen die einen Zwischenschritt benötigen (klassiche Transitivität), $p^3$ sind Verbindungen mit zwei transitiven Zwischenschritten, etc.
$p^*$ ist alles was man über beliebig viele Zwischenschritte erreichen kann. Es ist die Vereinigung von allen $p^n$.
Eigentlich nicht so deep…
Meet, Join, and Lattices
Meet: Alle Paare zweier Punkte im Hasse-Diagram haben einen eindeutigen gemeinsamen lower bound
Join: Alle Paare zweier Punkte im Hasse-Diagram haben einen eindeutigen gemeinsamen upper bound
Lattice: Alle Paare haben Meet und Join