Es gibt ein einziges Element, aus dem durch wiederholtes Anwenden der Gruppenoperation alle Elemente der Gruppe entstehen.
Beispiele:
$\mathbb{Z}$ = $〈1〉$
$\mathbb{Z}_{7}^{*}$ = $〈3〉$, also {3,2,6,4,5,1} (mit 3 hoch steigendem n kommt man mod 7 auf alle Restklassen)
- Lagrange: H ist eine Untergruppe von G (endlich). |H| teilt |G|.
- Die Ordnung des Generators muss gleich der Gruppenordnung sein (bei endlichen Gruppen)
- ord(a) divides |G| for every a ∈ G
- Unter Addition modulo 8 muss für einen Generator $\gcd(k,8) = 1$ gelten.
- Gruppe G ist zyklisch, wenn $g \in G$ existiert mit $〈g〉=G$. Somit $\text{ord(g)}=|G|$.
- A cyclic group of order n is isomorphic to〈$\mathbb{Z}_{n}$; ⊕〉, siehe Vorlesung
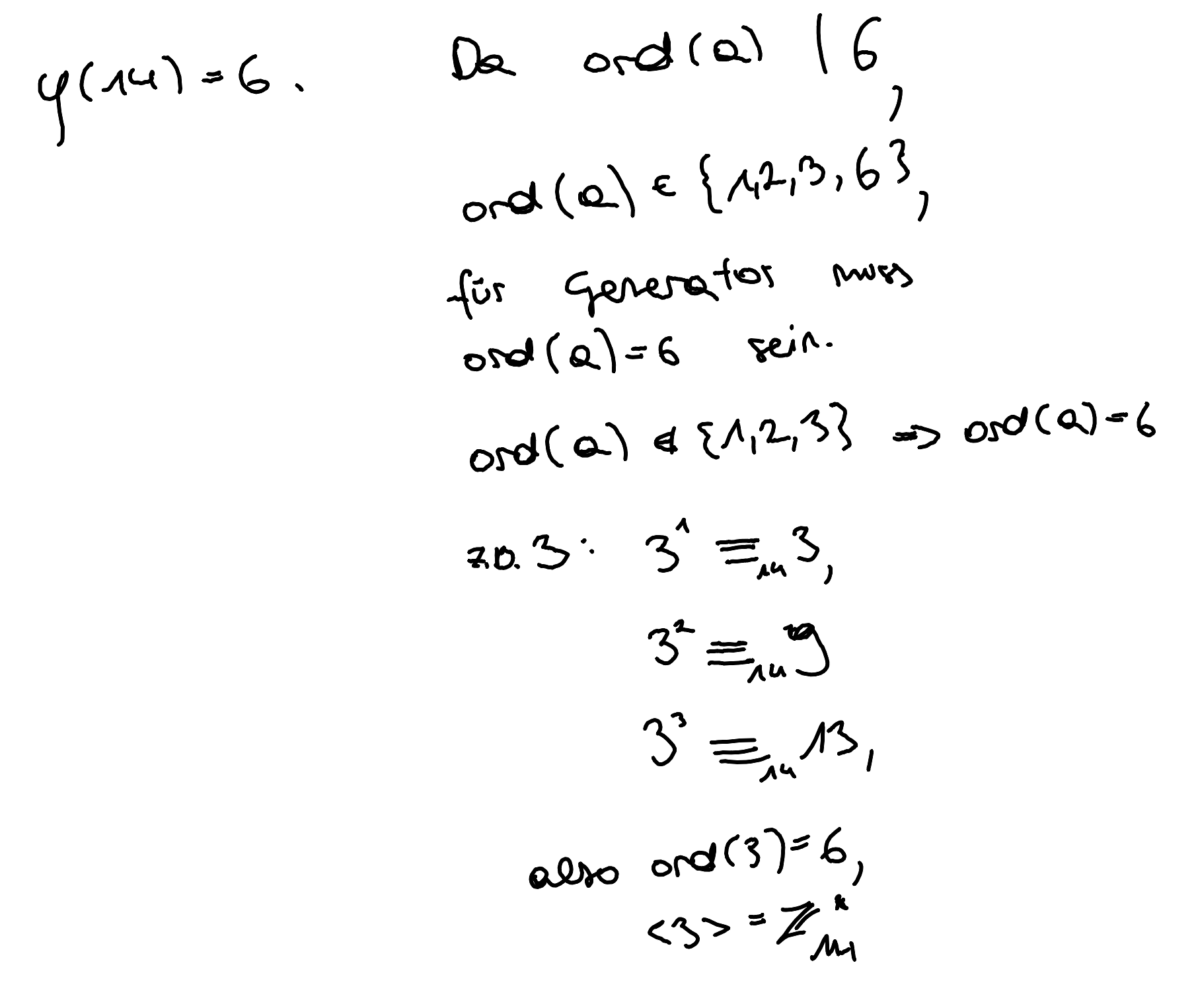

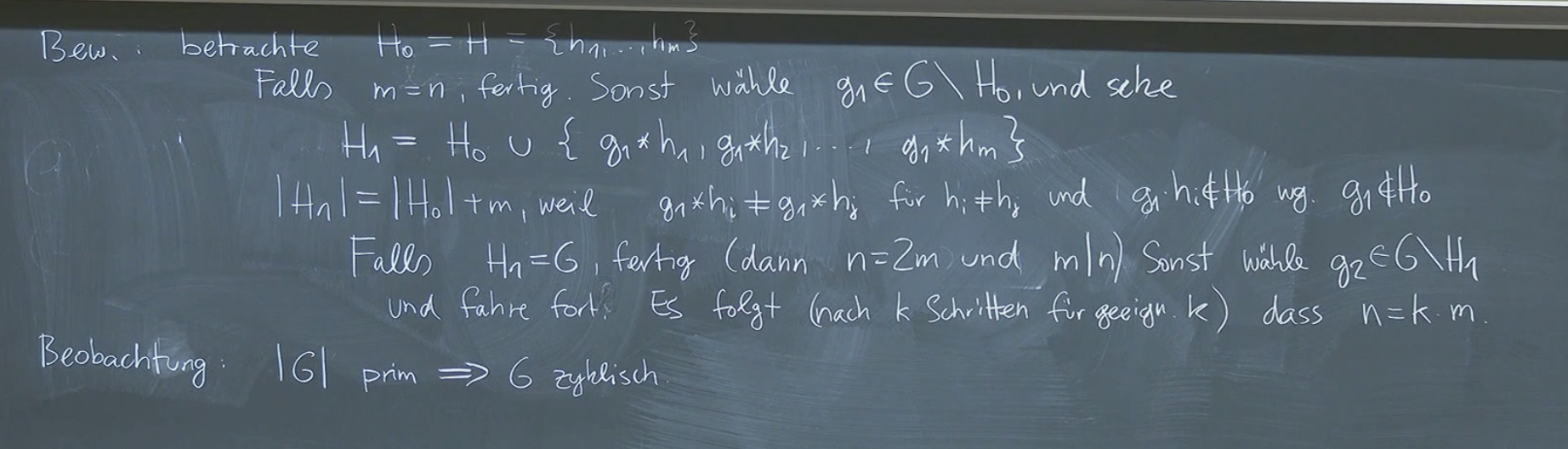
Weiter mit → Euler