Quick Facts
$$
A^T A \text{ invertierbar} \iff A \text{ hat linear unabhängige Spalten}.
$$
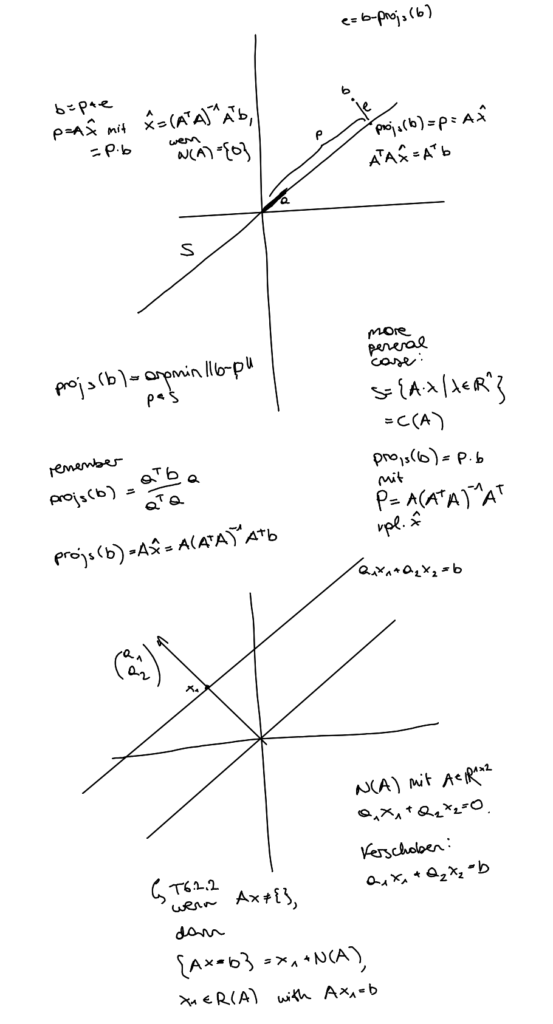
Ist $S$ der von den Spalten von $A$ erzeugte Raum. Es gilt:
$$
\operatorname{proj}_S(b)=A(A^T A)^{-1}A^T b,\qquad
P=A(A^T A)^{-1}A^T.
$$
P ist die Projektionsmatrix. Für in-depth Informationen, siehe Least Squares und Lineare Regression.
Beispiel: Projektion Vektor auf Ebene
Gegeben:
$$
\mathbf u=(1,1,-1),\quad
\mathbf v=(1,7,11),\quad
\mathbf w=(4,2,6)
$$
Unterraum:
$$
S=\operatorname{span}{\mathbf u,\mathbf v}
$$
Schritt 1: Matrix $A$
$$
A = \begin{pmatrix}
1 & 1 \\
1 & 7 \\
-1 & 11
\end{pmatrix}
$$
Schritt 2: Produkt
$$
A^T A = \begin{pmatrix}
3 & -3 \
-3 & 171
\end{pmatrix}
$$
Schritt 3: Berechnung des Koeffizientenvektors
$$
x = (A^T A)^{-1} A^T w
= \begin{pmatrix} \tfrac{1}{2} \ \tfrac{1}{2} \end{pmatrix}
$$
Schritt 4: Projektion
$$
\operatorname{proj}_S(w)
= A x
= \tfrac{1}{2}(u+v)
= \begin{pmatrix} 1 \ 4 \ 5 \end{pmatrix}
$$
$$
r = w – \operatorname{proj}_S(w)
= \begin{pmatrix} 3 \ -2 \ 1 \end{pmatrix}
$$
Norm:
$$
\|\mathbf r\|=\sqrt{3^2+(-2)^2+1^2}=\sqrt{14}
$$
Orthogonalitätsprüfung:
$$
\mathbf r\cdot \mathbf u = 0,\qquad \mathbf r\cdot \mathbf v = 0
$$
Beispiel: Winkel zwischen $\mathbf w$ und seiner Projektion
$$\cos\theta = \frac{\mathbf w\cdot\operatorname{proj}_S(\mathbf w)} {\|\mathbf w\|\ \|\operatorname{proj}_S(\mathbf w)\|} = \frac{\sqrt{3}}{2}$$
Damit:
$$
\theta=30^\circ
$$