13.11.2025
Begriffe
Definition:
Graph mit geordneten Paaren
Knoten haben Nachfolger und Vorgänger, Eingangsgrad und Ausgangsgrad.
Senke:
Knoten ohne Nachfolger, $\text{deg}_{out}(v)=0$
$\nexists \text{ Zyklus} \implies \exists \text{ Senke}$
Quelle:
Knoten ohne Vorgänger, Beginn einer topologischen Reihenfolge, $\text{deg}_{in}(u)=0$
gerichteter Zyklus:
gerichteter Weg mit erster Knoten = letzter Knoten
gerichteter Pfad:
kein Knoten wiederholt
Darstellung von Graphen
Adjazenzmatrix
Matrix: jede Zeile steht für einen Knoten. Wenn in einer Spalte in dieser Zeile eine 1 steht, so ist die Spalte ein Nachfolger von der Zeile
$$
A_{uv} =
\begin{cases}
1 & \text{falls } (u,v) \in E \\
0 & \text{sonst}
\end{cases}$$
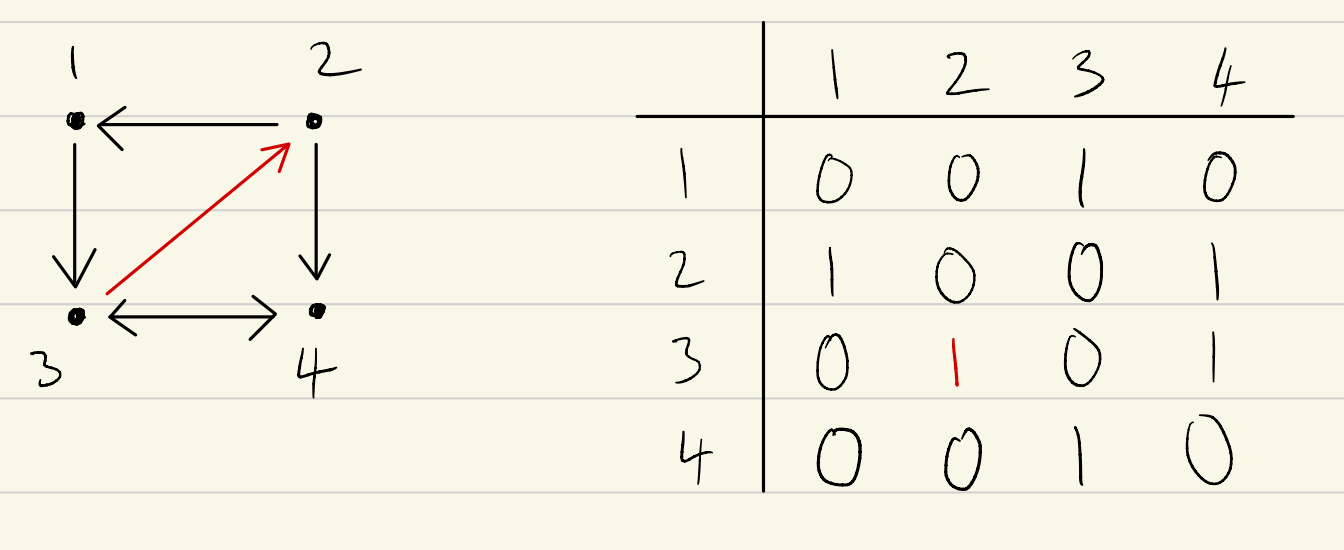
Adjazenzliste
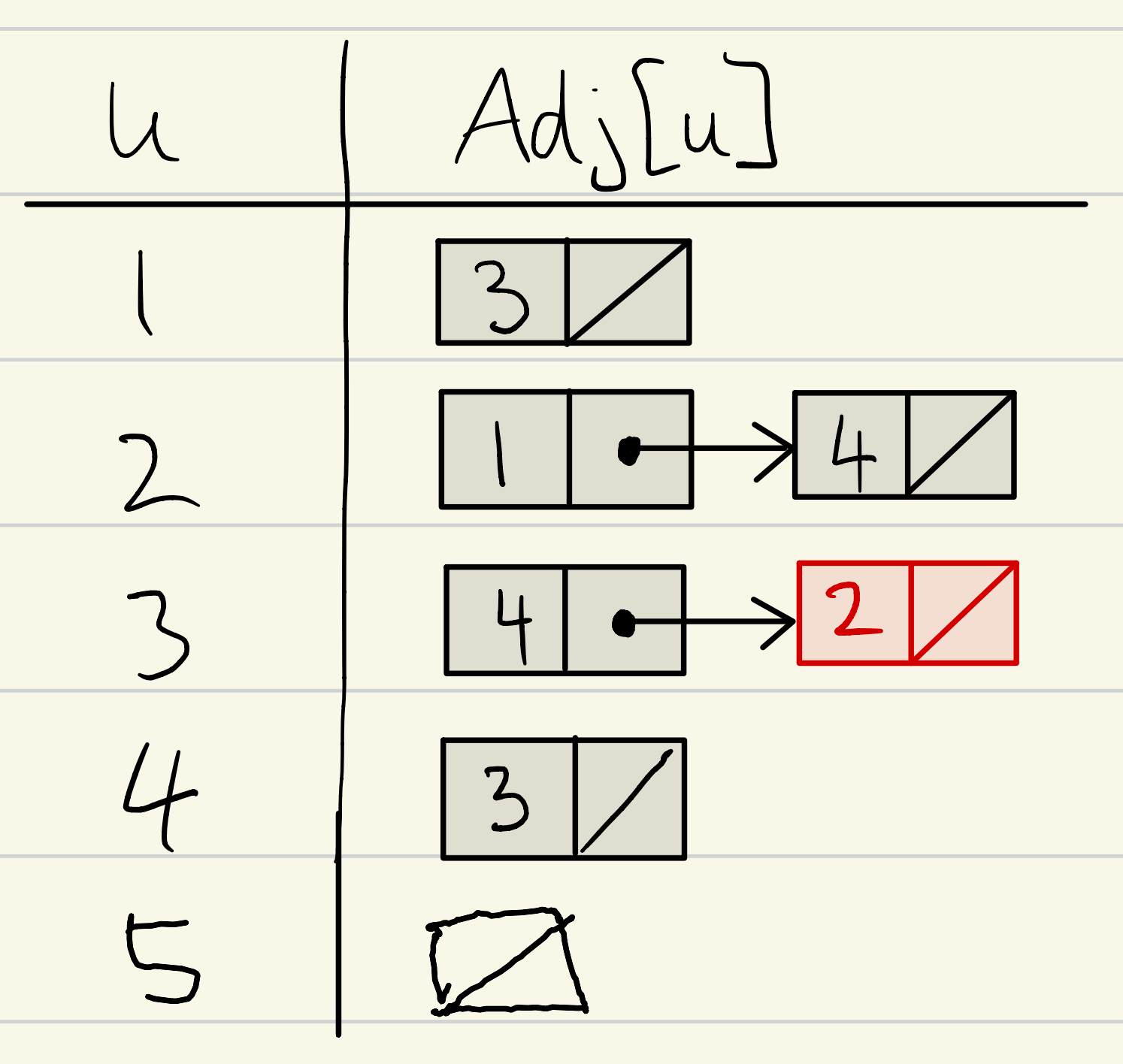
- Einfach verkettete Liste für jedes
u Adj[u] = Liste aller Nachfolger von u- Reihenfolge der verketteten Elemente (Nachfolger) beliebig
Laufzeiten
| Operation | Adjazenzmatrix | Adjazenzliste |
|---|---|---|
| teste $(u,v) \in E$ | $\mathcal{O}(1)$ | $\mathcal{O}(1 + \deg_{out}(u))$ |
| zähle alle Nachfolger von $u$ | $\Theta(n)$ | $\Theta(\deg_{out}(u))$ |
| Tiefensuche | $\mathcal{O}(n^2)$ | n+|E| |
- $\deg_{out}(u)$ ist die Länge der Liste (“Anzahl Spalten in der u-Zeile”). +1, da wenn die Liste leer ist (siehe Beispiel 5 im Bild oben), hätten wir sonst $O(0)$, was nicht möglich ist